Recursive
(RECURSION) adalah proses pengulangan sesuatu dengan cara kesamaan-diri. Sebagai contohnya, saat dua cermin berada paralel antara satu dengan yang lain, gambar yang tertangkap adalah suatu bentuk rekursi tak-terbatas. Istilah ini memiliki makna beragam bergantung kepada ragam disiplin mulai dari linguistik sampai logika. Penggunaan paling umum dari rekursi yaitu dalam matematika dan ilmu komputer, yang mengacu kepada suatu metode mendefinisikan fungsi yang mana fungsi tersebut menggunakan definisinya sendiri. Secara spesifik hal ini mendefinisikan suatu instansi tak-terbatas (nilai fungsi), menggunakan ekpresi terbatas dengan beberapa instansi bisa merujuk ke instansi lainnya, tapi dengan suatu cara sehingga tidak ada perulangan atau keterkaitan tak-terbatas dapat terjadi. Istilah ini juga digunakan secara umum untuk menjelaskan suatu proses pengulangan objek dengan cara kesamaan-diri.
Definisi formal dari rekursi
Rekursi dalam program perekaman layar, dengan suatu jendela paling kecil mengandung foto keseluruhan layar.
Dalam matematika dan ilmu komputer, kelas dari objek atau metode memperlihatkan perilaku rekursif bila mereka dapat didefinisikan oleh dua properti berikut:
- Sebuah kasus (atau beberapa kasus) dasar sederhana
- Sejumlah aturan yang mengurangi kasus-kasus lainnya sampai ke kasus dasarnya.
Sebagai contoh, berikut ini adalah definisi rekursif dari leluhur seseorang:
- Orang tua seseorang adalah leluhur seseorang (kasus dasar).
- Orang tua dari suatu leluhur juga merupakan leluhur-nya (langkah rekursi).
Bilangan Fibonacci adalah contoh klasik dari rekursi:
- Fib(0) adalah 0 [kasus dasar]
- Fib(1) adalah 1 [kasus dasar]
- Untuk semua integer n > 1: Fib(n) adalah (Fib(n-1) + Fib(n-2)) [definisi rekursif]
Banyak aksioma matematika berdasarkan aturan-aturan rekursif. Sebagai contohnya, definisi formal dari bilangan asli pada Aksioma Peano dapat dideskripsikan sebagai: 0 adalah bilangan asli, dan setiap bilangan asli memiliki sebuah suksesor, yang juga merupakan bilangan asli. Dengan kasus dasar ini dan aturan rekursif, seseorang dapat membuat himpunan dari semua bilangan asli.
Gambaran humornya berbunyi: “Untuk memahami rekursi, pertama anda harus memahami rekursi.” Atau mungkin yang lebih akurat, dari Andrew Plotkin: “Jika anda telah mengetahui apa itu rekursi, cukup ingat jawabannya. Kalau tidak, cari orang yang berdiri paling dekat dengan Douglas Hofstadter selain anda; lalu tanya dia rekursi itu apa.”
Objek matematika yang didefinisikan secara rekursif termasuk fungsi, himpunan, dan terutama sekali fraktal.
Rekursi dalam matematika
Segitiga Sierpinski—sebuah rekursi terbatas dari segitiga membentuk suatu jeruji geometris.
Himpunan yang didefinisikan secara rekursif
Contoh: bilangan asli
Contoh kanonikal dari himpunan yang didefinisikan secara rekursif yaitu diberikan oleh bilangan asli:
0 ada dalam
jika n ada dalam , maka n + 1 ada dalam
Himpunan dari bilangan asli adalah himpunan terkecil yang memenuhi dua properti sebelumnya.
Contoh: himpunan dari proposisi benar terjangkau
Contoh menarik lainnya adalah himpunan dari semua proposisi “benar terjangkau” dalam suatu sistem aksioma.
- Jika suatu proposisi adalah sebuah aksioma, maka ia adalah suatu proposisi benar terjangkau.
- Jika suatu proposisi dapat dihasilkan dari proposisi benar terjangkau dengan menggunakan aturan-aturan inferensi, maka ia adalah proposisi benar terjangkau.
- Himpunan dari proposisi benar-terjangkau adalah himpunan terkecil dari proposisi yang memenuhi kondisi tersebut.
Himpunan ini disebut ‘proposisi benar terjangkau’ karena dalam pendekatan non-konstruktif terhadap fondasi matematika, himpunan dari proposisi benar bisa lebih besar daripada himpunan yang dibangun secara rekursif dari aksioma-aksioma dan aturan-aturan inferensi.
Contoh klasik dari rekursi adalah definisi dari fungsi faktorial, diberikan dalam kode C:
unsigned int factorial(unsigned int n)
{
if (n == 0) {
return 1;
} else {
return n * factorial(n-1);
}
}
Teorema rekursi
Dalam teori himpunan, ini adalah teorema yang menjamin bahwa fungsi yang terdefinisi secara rekursif itu ada. Diberikan suatu himpunan X, sebuah elemen a dari X dan sebuah fungsi , teorema menyatakan bahwa ada fungsi unik (dengan menunjukkan himpunan dari bilangan asli termasuk nol) sehingga
untuk setiap bilangan asli n.
Pembuktian keunikan
Ambil dua fungsi dan sehingga:
dengan a adalah elemen dari X.
Ia dapat dibuktikan dengan induksi matematika bahwa untuk semua bilangan asli n:
Kasus dasar: sehingga persamaan memenuhi untuk .
Langkah Induktif: Misalkan untuk beberapa . Maka
Karenanya F(k) = G(k) menyiratkan F(k+1) = G(k+1).
Dengan induksi, untuk semua .
Contoh-contoh
Beberapa relasi perulangan umum yaitu:
Dalam matematika, faktorial dari bilangan asli n adalah hasil perkalian antara bilangan bulat positif yang kurang dari atau sama dengan n. Faktorial ditulis sebagai n! dan disebut n faktorial. Secara umum dapat dituliskan sebagai:
Sebagai contoh, nilai dari adalah Berikut ini adalah daftar sejumlah faktorial :
n n!
0 1
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
10 3628800
12 479001600
14 87178291200
16 20922789888000
18 6402373705728000
20 2432902008176640000
25 1.5511210043×1025
42 1.4050061178×1051
50 3.0414093202×1064
70 1.1978571670×10100
100 9.3326215444×10157
450 1.7333687331×101.000
1000 4.0238726008×102.567
3249 6.4123376883×1010.000
10000 2.8462596809×1035.659
25206 1.2057034382×10100.000
100000 2.8242294080×10456.573
205023 2.5038989317×101.000.004
1000000 8.2639316883×105.565.708
Fungsi faktorial didefinisikan sebagai:
Selain definisi tersebut, terdapat juga definisi secara rekursif, yang didefinisikan untuk
Untuk n yang sangat besar, akan terlalu melelahkan untuk menghitung n! menggunakan kedua definisi tersebut. Jika presisi tidak terlalu penting, pendekatan dari n! bisa dihitung menggunakan rumus Stirling:
Juga terdapat definisi analitik untuk faktorial, yaitu menggunakan fungsi gamma:
Finding Factorial of a Number in Java
The factorial of a number is defined is the product of natural numbers from one to that particular number. Mathematically,
n! = 1 * 2 * 3 * …. * (n-1) * n
For example, the factorial of 4 is
4! = 1 * 2 * 3 * 4 = 24
This article will explain you how to find the factorial of a number through iteration as well as recursion.
Finding factorial of a number in Java using Iteration
Let the number whose factorial is to be found be stored in the variable n. A new variable ‘result’ of type int is declared and initialised with the integer 1.
int result = 1;
Now, our task is to multiply the variable result with all natural numbers from 1 to n. For this purpose, we use a for loop with a counter i that ranges from 1 to n. Within the loop, the existing value of result will be multiplied with the loop counter.
for (int i = 1; i <= n; i++) {
result = result * i;
}
Let us take a small number n = 3 to understand how the above loop works. Before entering the loop, result would be initialised to one. The loop will execute thrice with the value of i = 1, 2 and 3. When the value of i becomes 4, the loop condition fails. When the value of i is 1, the existing result would be multiplied with 1 which again gives one. In the second iteration, result will be multiplied with 2 and in the third iteration with 3. These calculations are shown below:
result = 1
i = 1 result = result * i = 1 * 1 = 1
i = 2 result = result * i = 1 * 2 = 2
i = 3 result = result * i = 2 * 3 = 6
When the loop exists, the value result which was initially one would be already multiplied by all natural numbers from 1 to n. Thus, result holds the factorial of the number.
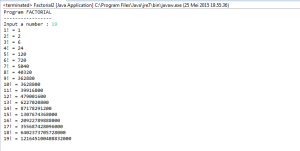
Given below is a program which finds the factorial of the number 7.
public class Factorial {
public static void main(String[] args) {
int n = 7;
int result = 1;
for (int i = 1; i <= n; i++) {
result = result * i;
}
System.out.println(“The factorial of 7 is ” + result);
}
}
The output of the above program would be
The factorial of 7 is 5040
We can start the loop counter, i from 2 instead of 1 because in the first iteration the value of result gets multiplied by 1 which again gives one. The modified loop can be written as
for (int i = 1; i <= n; i++) {
result = result * i;
}
We can also start the loop counter from n and decrement it till 2 or 1. In that case, the loop would look like
for (int i = n; i >= 1; i–) {
result = result * i;
}
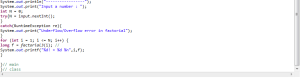
Given below is another program where the number whose factorial is to be calculated is taken as an input from the user and the result is displayed on the screen.
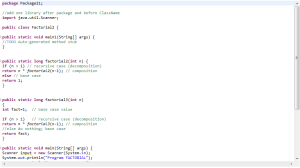
CONTOH CODING :
import java.util.Scanner;
public class Factorial {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print(“Enter the number whose factorial is to be found: “);
int n = scanner.nextInt();
int result = factorial(n);
System.out.println(“The factorial of ” + n + ” is ” + result);
}
public static int factorial(int n) {
int result = 1;
for (int i = 1; i <= n; i++) {
result = result * i;
}
return result;
}
}
Here is a sample execution
Enter the number whose factorial is to be found: 7
The factorial of 7 is 5040
Finding factorial of a number in Java using Recursion
The factorial of a number be found using recursion also. The base case can be taken as the factorial of the number 0 or 1, both of which are 1. The factorial of some number n is that number multiplied by the factorial of (n-1). Mathematically,
factorial ( 0 ) = 1
factorial ( n ) = n * factorial ( n – 1 )
Given below is a program which calculates the factorial of 7 using recursion.
public class Factorial {
public static void main(String[] args) {
int n = 7;
int result = factorial(n);
System.out.println(“The factorial of 7 is ” + result);
}
public static int factorial(int n) {
if (n == 0) {
return 1;
} else {
return n * factorial(n – 1);
}
}
}
Example:
publicclassTest{ publicstaticvoid main(String args[]){ double x=11.635; double y=2.76; System.out.printf(“The value of e is %.4f%n”,Math.E); System.out.printf(“pow(%.3f, %.3f) is %.3f%n”, x, y,Math.pow(x, y)); }}
This produces the following result:
The value of e is 2.7183pow(11.635, 2.760) is 874.008
Bilangan Fibonacci
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Dalam matematika, bilangan Fibonacci adalah barisan yang didefinisikan secara rekursif sebagai berikut:
Penjelasan: barisan ini berawal dari 0 dan 1, kemudian angka berikutnya didapat dengan cara menambahkan kedua bilangan yang berurutan sebelumnya. Dengan aturan ini, maka barisan bilangan Fibonaccci yang pertama adalah:
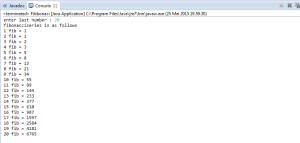
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946…
Barisan bilangan Fibonacci dapat dinyatakan sebagai berikut:
Fn = (x1n – x2n)/ sqrt(5)
dengan
Fn adalah bilangan Fibonacci ke-n
x1 dan x2 adalah penyelesaian persamaan x2 – x – 1 = 0.
Perbandingan antara Fn+1 dengan Fn hampir selalu sama untuk sebarang nilai n dan mulai nilai n tertentu, perbandingan ini nilainya tetap. Perbandingan itu disebut rasio emas yang nilainya mendekati 1,618.
Fibonacci number programs that implement this definition directly are often used as introductory examples of recursion. However, many other algorithms for calculating (or making use of) Fibonacci numbers also exist.
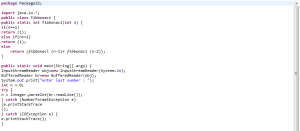
This simple java program uses recursion to print the first 10 Fibonacci numbers to the console.
<<Fibonacci.java>>=
public class Fibonacci {
public static int fib(int n) {
if (n < 2) {
return n;
}
else {
return fib(n-1)+fib(n-2);
}
}
}
Although it is based directly on the definition of a Fibonacci number, the recursive Fibonacci algorithm is extremely expensive, requiring time O(2n). It also performs a huge amount of redundant work because it computes many Fibonnaci values from scratch many times. A simple linear-time iterative approach which calculates each value of fib successively can avoid these issues:
public class FibonacciIterative {
public static int fib(int n) {
int prev1=0, prev2=1;
for(int i=0; i<n; i++) {
int savePrev1 = prev1;
prev1 = prev2;
prev2 = savePrev1 + prev2;
}
return prev1;
}
}
CONTOH CODING FACTORIAL :
HASIL CODING :
CONTOH CODING FIBONACCI :
HASIL CODING :